Primer Teorema de Tales
Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos se llaman semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, a saber, que:
|
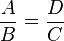
Segundo teorema
El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a lostriángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:
|
Este teorema es un caso particular de una propiedad de los puntos cocíclicos y de la aplicación de losángulos inscritos dentro de una circunferencia.




